الوسم: إنحناء، تقوس، تحدب

يتسبب الانكسار في الغلاف الجوي في ظهور جسم بعيد أعلى من موضعه الفعلي. ونتيجة لذلك ، يمكن أن يكون الجسم موجودًا فعليًا خلف انحناء الأرض ، ولكنه لا يزال مرئيًا نظرًا لانكسار الضوء الناتج عن الغلاف الجوي.

هناك العديد من الآلات الحاسبة الانحناء وأدوات المحاكاة التي لا تأخذ في الاعتبار الانكسار. تعطي نتائج صحيحة التي تشير إلى المواضع الفعلية للجسم ولكن لا تعطيك الوضع الظاهري الصحيح للجسم أثناء المشاهدة البصرية.

غالبًا ما يشعر المسطحين بالسعادة لأنهم يرون الآلة الحاسبة تعرض لهم النتائج التي يريدون رؤيتها ولا يرون سبب هذا التناقض.

للقيام بهذا “البحث” ، المسطحين يستعملون ملاحظات أو الصور الموجودة. ثم يضعون ارتفاع ومسافة المراقب والجسم باستخدام آلة حاسبة الانحناء على الإنترنت. إذا كان الجسم مرئيًا ، ولكن حسب الآلة الحاسبة ، فيجب أن يكون بالكامل خلف الأفق ، ثم يستدل بسرعة شديدة بأنه لا يوجد “انحناء”.

هم مخطئون. يرجع التباين إلى حقيقة أن الآلة الحاسبة لا تأخذ في الاعتبار الانكسار في الغلاف الجوي.

الغلاف الجوي هو ديناميكي ، وكذلك الانكسار الذي ينتج عنه، تتغير درجة الانكسار مع الوقت والظروف. معظم الآلات الحاسبة الانحناء التي تأخذ في الاعتبار الانكسار توفر خانة لتسجيل درجة الانكسار في الآلة الحاسبة.

ومن المفارقات أن العديد من هذه الملاحظات والصور تُظهر بوضوح أن انحناء الأرض يمنع رؤية الأجزاء السفلية من الأجسام ، ولكن لسبب ما المسطح لا يرى ذلك. هذا الدليل أكثر من كافي للسماح لنا أن نستنتج أن الجسم يختفي وراء انحناء الأرض ، حتى لو كانت الأجزاء العلوية من الجسم مرئية.

بعض حاسبات الانحناء على الانترنت الأكثر شيوعاً

هذه لا تأخذ في الاعتبار الانكسار:
Earth Curve Calculator (dizzib.github.io)
Earth Curvature Calculator (earthcurvature.com)
GeoGebra Horizon Calculator (geogebra.org)

هذه تأخذ الإنكسار في اإعتبار :

Earth Curvature Calculator (physicsstuff.000webhostapp.com)
Metabunk: Earth’s Curve Horizon, Bulge, Drop, and Hidden Calculator (metabunk.org)
FEI Horizon Calculator (flatearthinsanity.blogspot.com)
Curvature App: Simulation of Globe-Earth and Flat-Earth (walter.bislins.ch)

يعتمد إختفاء أسفل الجسم البعيد الناتج عن انحناء الأرض على:

1) المسافة إلى الجسم المرصود.

2) إرتفاع الراصد.

3) ارتفاع الجسم المرصود.

4) الانكسار في الغلاف الجوي.

يحب المسطحين استخدام رؤية الأجسام البعيدة لإثبات أن انحناء الأرض غير موجود. في كثير من الأحيان ، لا يأخذ المسطح في الاعتبار ارتفاع الراصد وانكسار الغلاف الجوي ، او إرتكاب أخطاء أخرى ، مثل أخطاء تحويل الوحدات وحساب المسافات وما إلى ذلك. بمجرد أن يتم أخذ كل شيء في الاعتبار وتصحيح الأخطاء ، فإن كل شيء سيتطابق مع الأرض الكروية.

الخطأ الأكثر شيوعًا هو عدم مراعاة إرتفاع المراقب. فهم يحسبون فقط الأنخفاض من المستوى الأفقي. وبغض النظر عما إذا كانوا يستخدمون AutoCAD 2016 بدقة تصل إلى 15 رقمًا ، فإن الأرقام ستكون غير صحيحة إذا كانت الهندسة غير صحيحة في المقام الأول.

الخطأ الثاني الأكثر شيوعًا هو عدم مراعاة الانكسار في الغلاف الجوي. عادةً ما يكسر الغلاف الجوي الضوء ليتبع انحناء الأرض إلى حد ما ويجعل الأشياء تظهر فوق الأفق أكثر مما هي عليه في الواقع. يمكن أن يُظهر الانكسار في الغلاف الجوي الأجسام التي تكون وراء الأفق.

ينبغي التأكيد على أن الانكسار في الغلاف الجوي ليس ثابتًا. ذلك يعتمد على الظروف المناخية. يمكن أن يختلف مقدار الانكسار حتى في يوم واحد.

وبمجرد أخذ كل شيء في الاعتبار وتصحيح جميع الأخطاء ، سيكون كل شيء متوافقا مع نموذج الأرض الكروية. في كل مرة.

“استخدام AutoCAD 2016 مع 15-Digit Accuracy”

ما يلي هو مخطط انحناء الأرض الأسطوري الذي تم تصميمه من طرف أحد المسطحة، باستخدام “أوتوكاد 2016 بدقة 15-Digit”. على الرغم من أن هذا الرسم البياني غير دقيق من الناحية الفنية ، فإنه غالباً ما يتم استخدامه بطريقة مبالغ فيها من قبل المسطحين لحساب المقدار المتوقع من الإنحجاب تحت الأفق drop عندما يكون غير ملائم لهذا الغرض ، وهو في الواقع لا يُستعمل كثيرًا في أي موضع آخر.

.

References #مراجع
Curvature App – Walter Bislin, the best tool for calculating and simulating Earth’s curvature.
Atmospheric refraction – Wikipedia

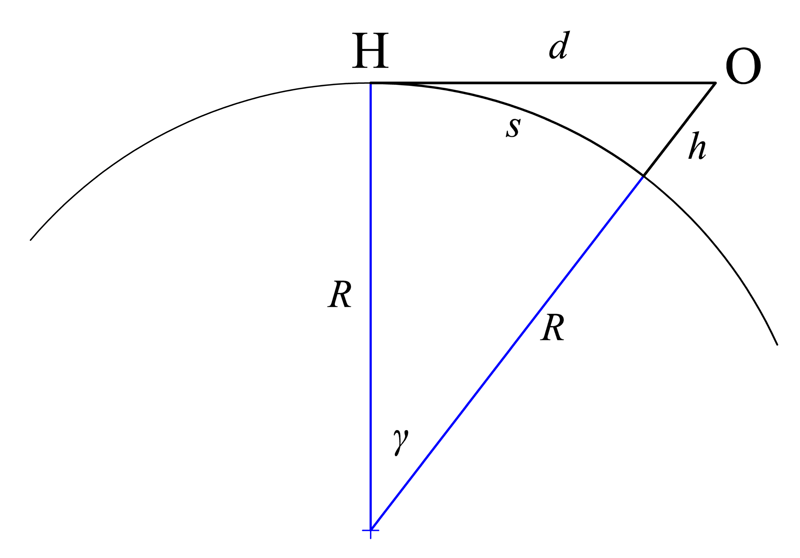
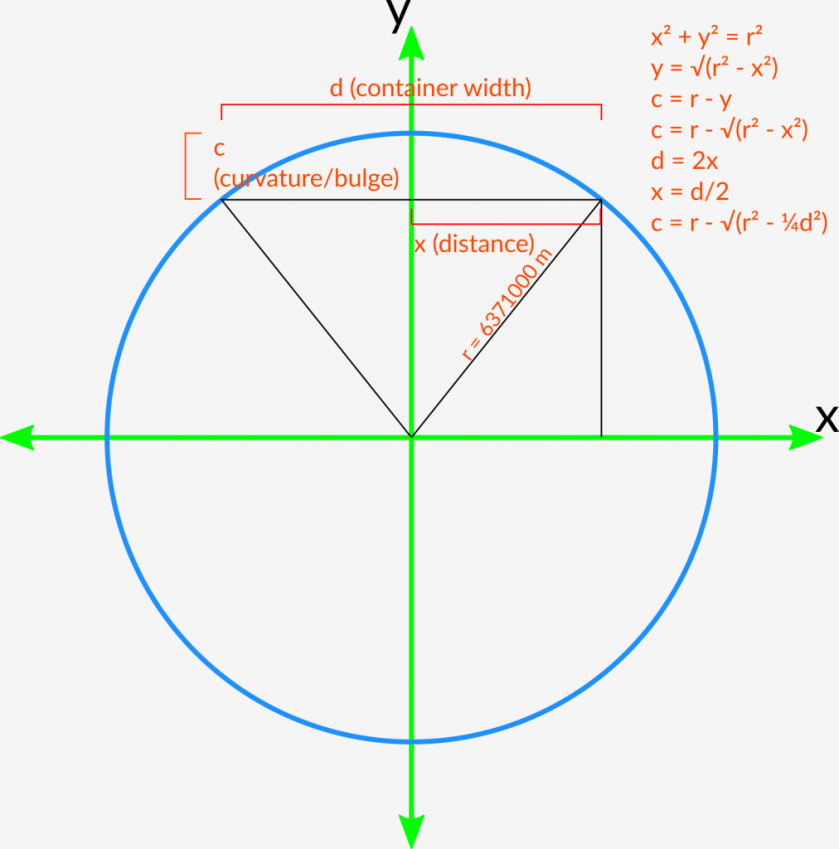
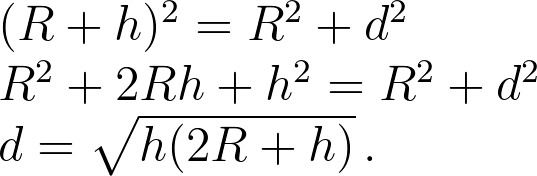بحيرة بونتشارترين هي بحيرة في لويزيانا في الولايات المتحدة، فيها أبراج نقل الطاقة الكهربائية لحوالي 24.27 كم (15 ميل) تربط بين الضفتين وهي مستقيمة ومتشابهة وعلى نفس الارتفاع ، مما يجعل هذه الأبراج مثالية لرصد انحناء الأرض.

تم نشرها لأول مرة بواسطة Soundly ، الذي قدم دليلاً على انحناء الأرض باستخدام سلسلة من الصور ومقاطع الفيديو لهذا الخط الناقل للطاقة في يونيو 2017. ومنذ ذلك اليوم ، أصبحت الأبراج و البحيرة المكان الأكثر شعبية للسياحة العالمية.

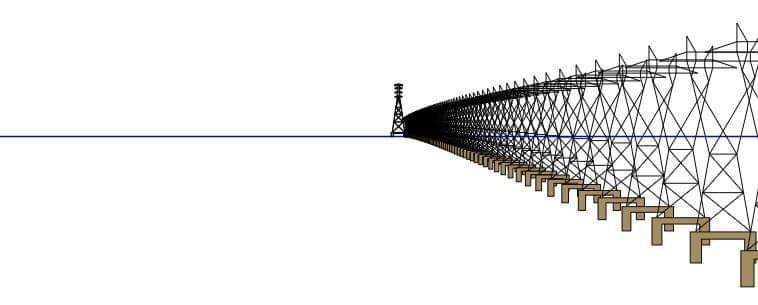
لا تتطلب الصور ومقاطع الفيديو نفسها أي تفسير لأنها تظهر بوضوح الانحناء. ولكن هنا نضيف خطوط منظور للتأكيد على الانحناء. إذا كانت الأرض مسطحة ، فإن نقطة التلاشي يجب أن تكون تتقاطع مع الأفق. لكنهم بوضوح فوق الأفق. هذا الواقع يبين لنا إنخفاض الأفق ويثبت انحناء الأرض.

1) “لكن ، الأبراج ليست مستقيمة!”

هناك اعتراضات من طرف ضحايا الأرض المسطحة. يقول البعض أن الأبراج ليست مستقيمة.

قام أحد المسطحين وهو رجل عديم الضمير على YouTube ، بعمل ما يسمى بـ “التحليل” على مجموعة مختلفة من الأبراج ، والتي ليست مستقيمة وتغطي مسافة أقل بكثير. للأسف ، لم يقم بنشر مقطع الفيديو الخطأ التابع له مطلقًا ، ولا يزال الفيديو التابع له على YouTube يؤدي إلى تضليل المشاهدين الأبرياء.

حسنا الملاحظات تثبت أن الأعمدة مستقبمة من كلا الجانبين. إذا لم تكن مستقيمة ، سيكون من الواضح جدا في الصور. لكن في الواقع ، تُظهر الصور نفس الانحناء.

يمكن التحقق من حقيقة أن الأبراج في خط مستقيم بإستعمال Google Earth.

2) “لكن ، الصور مزيفة!”

يمكن لأي شخص البحث على Google باستخدام كلمات “Pontchartrain Lake Powerlines” ، ومن السهل مشاهدة صور مماثلة التقطها أشخاص مختلفون ، على مدار فترات زمنية مختلفة.

أخذنا الصورة من مجموعة Soundly (Google Drive). نحن نستخدم صورة IMG_4118.JPG. كما يوفر ملف RAW بتنسيق Canon CR2: IMG_4118.CR2.

لا يوجد برنامج قياسي يمكنه إنشاء ملف CR2. إذا أراد شخص ما محاكاة ملف CR2 ، فعليه إنشاء برنامج خاص به. ستكون مهمة ضخمة لمحاكاة هذه الصورة.

بصراحة Soundly نفسه توقع تكذيب طرف ثالث عديم الضمير يتهمه بفعل أشياء سيئة. ولهذا ، قام بعمل كل شيء مباشرة على YouTube ، من التقاط الصور إلى التنزيل عبر الإنترنت.

في النهاية ، يمكن التحقق من المعلومات وقابلة للتزييف. كل شخص حر في زيارة الأبراج والتحقق بنفسه.

3) “الأبراج قريبة جدا من بعضها البعض!”

تظهر الأبراج قريبة من بعضها البعض بسبب تأثير ضغط téléobjectif. وكلما كان البعد البؤري للعدسة أكبر ، كلما اقتربت الأجسام من بعضها البعض. وتبدو كذلك أكثر شبهاً بالحجم.

التقط الصورة باستخدام عدسة Canon 75-300mm على كاميرا Canon 1300D. استخدم البعد البؤري 300 ملم. كاميرته لديها غالق بسرعة 1.6 ×. وبالتالي ، العدسة تساوي 480mm على كاميرا 35mm. باستخدام هذه المتغيرات ، يمكننا حساب أن مجال الرؤية الأفقي هو حوالي 4.3 درجة. للمقارنة عين الإنسان لديها مجال الرؤية الأفقية حوالي 55 درجة، يظهر عرض من تأثير ضغط المقراب. عندما يصبح البعد البؤري أطول ، يكون حجم الأجسام ومظهرها أقرب إلى بعضها البعض. الأكواب هنا هي بنفس الحجم ولم يتم تحريكها أثناء التصوير.

في الواقع ، تبلغ المسافة بين الأبراج 287 م.

4) “لكن ليس هناك تقوس أفقي واضح!”

إذا استطعنا البرهنة على وجود الانحناء ، فلماذا لا نرى تقوساً في الافق؟ للحصول على إجابة لهذا السؤال ، قم أولاً بحساب المسافة الأفقية في الصورة.

وفقا للبيانات الوصفية EXIF ، استخدم Soundly عدسة 75-300mm على كاميرا كانون 1300D. التقط الصورة ببعد بؤري 300 ملم. الكاميرا لديها سرعة غالق 1.6 ×. من هذه القيم ، يمكننا حساب أن مجال الرؤية الأفقي يبلغ حوالي 4.3 درجة.

بافتراض أن المسافة إلى الأفق هي 20 كم (المسافة إلى البرج الأخير أكبر من 24 كم) ، يمكننا بعد ذلك حساب المسافة الأفقية في الصورة = 20 كم × جيب 4.3 ° = ± 1.5 كم.

صورة Soundly تملك نسبة عرض إلى ارتفاع rapport d’aspect 3: 2. بعد الإقتصاص 1: 1 ، تكون المسافة الأفقية في الصورة حوالي 1 كم فقط. ليس من الواقعي ملاحظة الانحناء على هذه المسافة الصغيرة.

5) “لا تظهر الصورة المقدار الصحيح للانحناء!”

يمكننا التحقق من ذلك باستخدام تطبيقات المحاكاة ل Walter Bislin تطبيق المحاكاة . يحاكي التطبيق انحناء الأرض باستخدام الحجم الفعلي للأرض ويقارنه في نفس الوقت بنموذج مسطح افتراضي.

يمكننا ملاحظة أن نتيجة المحاكاة تطابق تمامًا جميع الصور ومقاطع الفيديو التي نشرها Soundly.

6) “هناك شريط فيديو يظهر المشهد نفسه ، ولكن الانحناء ليس موجود!”

يمكن أن يجعل انكسار الضوء في الغلاف الجوي جسمًا بعيدًا فعليًا خلف الإنحناء لا يزال مرئيًا. تحدث هذه الظاهرة لأن الهواء الأقرب إلى السطح له ضغط أعلى من الهواء الأبعد من السطح ، مما يسبب إنحناء لمسار الضوء على طول انحناء الأرض ، إلى حد معين.

مقدار الانكسار يعتمد على المناخ. في حالاته القصوى ، قد يكون الانكسار شديدًا ويعطي انطباعًا بأن أبراج الإرسال مستقيمة.

يُظهر مقطع فيديو هذه الظاهرة والمسطحين يستخدمها بكثرة “كدليل” على أنه لا يوجد تقوس. يمكننا رؤية الضباب في الفيديو ، مما يدل على أن الطقس ليس واضحًا مثل الصور ومقاطع الفيديو التي صورها Soundly. إذا حاول مخرج الفيديو تسجيل المشهد نفسه في أيام مختلفة وفي أوقات مختلفة من اليوم ، فسيحصل بسهولة على شيء مشابه لـ Soundly. حتى أنهم قد فعلوا ذلك ، لكنهم يفضلون فقط الدليل الذي يدعم معتقداتهم.

يمكن أن يؤخذ في الاعتبار النقص الظاهري للانحناء في مثل هذا الفيديو في النموذج الأرضي الكروي ويكون أكثر منطقية لكن ليس العكس. لا يمكن أبدًا تفسير وجود الانحناء في نموذج الأرض المسطحة.

نتيجة المحاكاة باستخدام الانكسار في حالته العادية

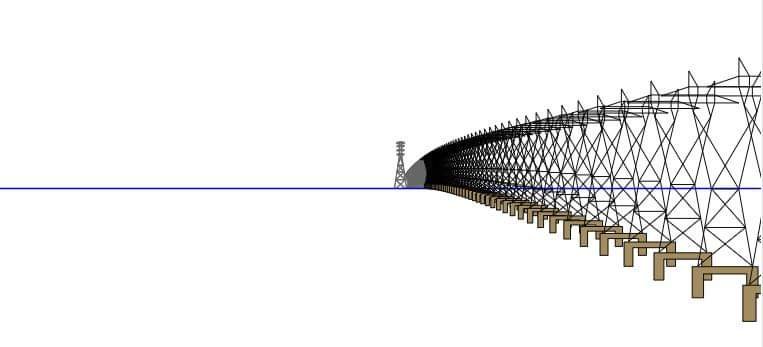
نتيجة المحاكاة باستخدام الانكسار في حالته القصوى

وكما يتبين ، يمكن بسهولة تفسير نتيجة المشهد في النموذج الأرضي الكروي.

7) “هناك مشهد يُظهر طريقًا ساخنا ومسطحًا مع صور معكوسة فوق!”

وتسمى هذه الظاهرة “سحابة الحرارة” أو “السراب” ، أي ظهور بريق أقل. إن اختلاف الضغط بين الهواء الدافئ على سطح الطريق والهواء البارد الأكثر كثافة أعلاه يخلق تدرجًا انكساريًا. ينكسر الضوء من الأجسام فوق الطريق ، مما يؤدي إلى ظهور الأشياء فوق الطريق.

لا تمثل نتيجة السراب المعروضة في الفيديو أي تشابه مع المشهد الذي صوره Soundly.

Référence #مراجع
Soundly’s pictures. Google Drive Link.
Curved Water Found – Lake Pontchartrain – Electrical Transmission Pylons – (Debunk Flat Earth) – Soundly
Soundly Shows Flat Earthers The Curve – Flat Earth Insanity
Flat Earth: Dr Zack can’t Pontchartrain – Sly Sparkane
Soundly Proving the Curvature of the Earth at Lake Pontchartrain – Metabunk
Curvature App: Transmission Line – Walter Bislin

تدفع الجاذبية المياه للبحث عن بذل أقل جهذ ممكن، والأمر الذي يسهل الامر هو الموقع الأقرب ما يمكن إلى مركز ثقل الأرض. ونتيجة لذلك ، سيكون سطح الماء سطحًا متساوي الجهد ويشكل سطحًا كرويًا تقريبًا يكون له نفس مركز ثقل الأرض. كل موقع على طول السطح لديه نفس الجهذ المبذول.

يصر المسطحين على أن الماء دائمًا ما يكون مستوٍ نظرًا لمشاهداتهم اليومية، ويستخلصون أن سطح الماء يكون مستوٍ دائمًا ، بغض النظر عن مساحة المسطح المائي، القول بهذا الاستنتاج هي مغالطة مفرطة.

في الواقع ، العكس هو الصحيح: الماء يشكل سطح كروي له نفس مركز ثقل الأرض، ولكن عندما تكون مساحة المسطح صغيرة نسبيًا ، يمكننا تقدير أن السطح مستو تقريبا، الانحناء موجود بلا شك، ولكنه صغير جدا و مهمل.

في منطقة واسعة جغرافيا ، مثل البحر أو المحيط ، لا يمكننا القول بالتقريب،
الماء المسطح تمامًا ليس متساويًا في الجهذ ولن يكون في حالة راحة أبدًا. سوف يأخذ في الإنسياب حتى يشكل سطحه انحناء له نفس مركز ثقل الأرض.

سطح الماء متساوٍ الجهذ : إنه مستوٍ ولكنه غير مسطح تماماً.

#مراجع

Equipotential – Wikipedia
Gravitational potential – Wikipedia

لا يوجد ملعب كرة قدم مصمم بشكل مستوٍ. الجزء الأوسط مرتفع قليلاً لتعزيز جريان المياه الزائدة. بدون هذا ، يمكن أن تصبح أرضية الملعب موحلة وغير مريحة.

وقد أجرى بعض المسطحين تجربة منظور “تقارب الخطوط المتوازية”. يضعون كاميرا على سطح ملعب كرة القدم ويسجلون شخصًا يمر بالميدان. ويبدأ الشخص يختفي من قدميه أولاً. ولأنهم ظنوا بأن ملعب كرة القدم كان مستوياً ، فقد توصلوا إلى استنتاج خاطئ بأن الشخص قد إختفى بسبب “المنظور”. كانوا مخطئين. في الواقع ، أرضية الملعب ليست مسطحة تمامًا. إذا كان مسطحًا تمامًا ، فسيظهر الشخص كاملاً في طرف الملعب.

#مراجع
Gestion du drainage – Université Cornell
Couronnes de terrain et drainage de surface – Ohio State University
Gazon vs. Herbe – Football Politique
Quelle est la couronne d’un terrain de football? – Sports Rec
Quandaries and Queries – Université de Regina
Manuel d’exigences pour les terrains de football – FIFA
Documents de classement au sol national de la FA – The FA
Pente – Wikipedia
CATÉGORIES ANALOGIE ,

قناة السويس هي ممر مائي يربط البحر الأبيض المتوسط بالبحر الأحمر. مستوى المياه في كل من البحرين هو نفسه تقريبا ، ولا تحتوي قناة السويس على نظام قفل.

يدعي المسطحين أن قناة السويس بنيت دون اعتبار للانحناء. وقالوا إنه إذا كانت الأرض كروية ، فيجب أن يكون مركز القناة على عمق 1666 قدمًا. هذا ببساطة مفهوم خاطئ. سطح الماء هو equipotentiel (متساوي الجهد) . إنها على بعد نفس المسافة من مركز جاذبية الأرض. ليس من الضروري حفر 1،666 قدمًا في وسط قناة السويس. يحتاج المهندسون فقط التأكد من أن قاعدة القناة تكون تحت مستوى سطح البحر بحيث يمكن أن تتدفق مياه البحر.

الاعتقاد الخاطئ أكثر من قرن من الزمان. في عام 1881 ، كتب سامويل رووبوثام في كتابه “الأرض ليست كرة” ، الطبعة الثانية”. في عام 1885 ، تحدث وليام كاربنتر ، مؤلف آخر للأرض المسطحة ،وعبر عن ذلك في كتابه “مائة دليل على أن الأرض ليست كرة”. في عام 1890 ، قام أليكس غليسون – المعروف بما يسمى “بالخريطة الأرض المسطحة” – بتوسيخ يديه هو الأخر ، ونشر فكرة خاطئة عن كتابه “هل الأرض كروية؟”. وبعد مرور أكثر من 100 عام ، كرر إيريك دوبي نفس الخطأ في كتابه “مؤامرة الأرض المسطحة” The Flat Earth Conspiracy.

كلهم ارتكبوا الخطأ نفسه عن طريق تفسير الخط المرجعي لقناة السويس ، والذي كان على عمق 6 أمتار تحت مستوى سطح البحر في وقت بناءه الأولي. يدعون أنه إذا كانت الأرض كروية ، فيجب حفر قناة السويس على خط مستقيم على ارتفاع 26 قدم تحت مستوى سطح البحر ، الأمر الذي يتطلب الحفر على عمق 1600 متر تحت مستوى البحر في وسط قناة السويس.

هم مخطئون. سطح الماء متساوٍ أو على نفس المستوى ، حتى عندما يعبر الماء قناة السويس. يحتاج المهندسون فقط إلى التأكد من أن عمق القاع يصل إلى 26 قدمًا ، بالنسبة إلى سطح équipotentielle لمياه البحر ، لأن سطح الماء ينحني ، فإن قاعدة القناة سوف تنحني أيضًا. على طول انحناء الأرض.

#مراجع

علم الفلك Zetetic ، الأرض ليست كرة – صامويل روبوتام

مائة دليل على أن الأرض ليست كرة – وليام كاربنتر

هل الأرض كروية؟ – ألكسندر جليسون

مؤامرة الأرض المسطحة – اريك دوباي

قناة السويس – ويكيبيديا

Equipotential: خاصية من سطح الماء – FlatEarth.ws

الأعلى هو كل نقطة أبعد عن مركز الأرض بالنسبة لمستوى سطح البحر، و العكس من ذلك، الأسفل هو النقطة الأقرب إلى مركز الأرض، بالنسبة إلى مستوى سطح البحر.
نقول ان نقطتان على نفس المستوى إذا كانتا في نفس الارتفاع بالنسبة لمستوى البحر.

بعض أنصار المسطحة غير قادر على فهم هذا. بالنسبة لهم ، “المستوى” يعني الإستواء ولكنهم مخطئون. في علوم الأرض ، يتم قياس الارتفاع من مستوى مرجعي ، عادة ما يكون مستوى سطح البحر.

من المفترض أن تكون كل من صفة المستوى، الإستقامية والإستواء والتسطح متناسبة مع كروية الأرض عند استخدامها في سياق سطح الأرض. القول بأن “خط السكة الحديد مستقيم بين لندن وليفربول” يعني أنه مستقيم على سطح الأرض ، بالنسبة إلى مستوى سطح البحر ، وليس مستقيماً كما هو الحال في “خط البصر”.

*في الصورة 1،2،3 و 4 كلها على نفس المستوى.
وكذلك 5،6،7 و 8 على نفس المستوى،
لكن 5،6،7،8 تعتبر أعلى مستوى من 1،2،3،4.

لكن المسطح يظن أن 5،2،7 يجب أن تكون على نفس المستوى مع 1،9،3. وهي في الحقيقة ليست على نفس الإرتفاع على مستوى البحر، وبهذا فهي ليست على نفس المستوى.

#المراجع

إرتفاع – ويكبيديا

الجيوديسي # مرتفعات – ويكيبيديا

المرتفعات – ويكيبيديا

فوق متوسط مستوى سطح البحر – ويكيبيديا

في بعض الأحيان يحتاج البحارة إلى تقدير مدى بعد أي جسم ما عنهم، وبدون رادارات، فإن الأفق هو النقطة المرجعية الوحيدة المتاحة بسهولة لتقدير المسافات.

من خلال معرفة ارتفاع المراقب على مستوى البحر ، يمكن حساب المسافة إلى الأفق ، وبالتالي تحديد المسافة إلى غاية هذا الجسم البعيد بالنسبة إلى الأفق، وهذا ممكن فقط لأن الأرض كروية.

* عندما يكون الجسم يظهر بالكامل و يكون تحت خط الأفق هذا يعني أنه أقرب من المسافة التي بين السفينة والافق.
*عندما يكون الجسم يظهر بالكامل ويكون على خط الأفق هذا يعني أنه على مسافة تساوي المسافة التي بين السفينة والافق.
*عندما يكون الجسم يظهر نصفه ويكون مخفي وراء الأفق هذا يعني أن الجسم ابعد من المسافة التي بين السفينة والأفق.

#مراجع

*دليل التدريب Lookout – الولايات المتحدة البحرية