التصنيف: تجارب

الانحناء الذي يظهر في صورة كرة يعتمد على 1. نصف قطر الكرة ، 2. مسافة الكاميرا من الكرة ، 3. مجال الرؤية للكاميرا ، و 4. خاصية تشويه الكاميرا المستخدمة .

كانت “لعبة تركيب الانحناء” هواية مفضلة عند المسطحين. يحاولون وضع صورة لتقوس الأرض مع صورة أخرى، فإذا وجدوا أن النتيجة غير صحيحة نسبيًا ، يسخرون منها. هم مخطئون.
يمكن التقاط صورتين مختلفتين للكرة بشكل مختلف وستظهر منحنى مختلفًا ، حتى إذا كان الجسم الكروي الذي يتم تصويره هو نفسه.

باستخدام هذا “المنطق” المسطح ، يمكننا التقاط صور لكرة السلة وكرة الجولف باستخدام عدستين مختلفتين للكاميرا ، ويمكننا “إثبات” بسهولة أن كرة السلة وكرة الغولف بنفس الحجم. لكننا نعرف أن كرة السلة أكبر بكثير من كرة الغولف.

يقوم المسطحين بعمل تجارب من هذا القبيل لأنهم بحاجة نفسية له.
عمليا ، يتعارض كل “تفسير” في مجتمع الأرض المسطحة مع الواقع وحتى التفاسير نفسها مع بعضها البعض. هذا سببه عدم الراحة الذهنية الكارثية، ثم يحاول تقليله بالتعبير عن ايجابات عاطفية سلبية. هذا هو السبب في نشر العديد من “معلومات الأرض المسطحة” في شكل ميمات عاطفية memes ، غالباً ما تسخر من “المعارضة”.

في هذه الحالة ، “لعبة تركيب الانحناء” هي التجربة التي يمكن يمكن لهم من خلالها أن يسخروا من شيء ما، وحقيقة أنه من السهل دحضها ليست مهمة بالنسبة لهم.

لمعان الشمس هو ضوء مشرق متلألئ يتكون عندما تنعكس أشعة الشمس على الأمواج أو أي سطح مائي. إن اي سطح متموج أملس مثل الماء مع الأمواج سيعكس أشعة الشمس بزوايا مختلفة عند كل نقطة على سطح الأمواج، ونتيجة لذلك ، سيشاهد الراصد من موقع مناسب العديد من الصور الصغيرة للشمس ، والتي تكونها أسطح الأمواج الصغيرة الموجهة بشكل مناسب لتعكس ضوء الشمس إلى الراصد.

يتخذ المسطحون الشكل الطويل لانعكاس غروب الشمس على سطح المحيط “كدليل” على أن الأرض مسطحة. هم مخطئون. لمعان الشمس هو نتيجة لتموج الماء. الفرق في الانحناء بين نموذج الأرض المسطح والكروي ليس بعيدا عن الفرق في شكل لمعان الشمس.

خلال غروب الشمس ، سيظهر لمعان الشمس على هيئة انعكاس طولي واحد بالقرب من الراصد وعلى طول المسافة إلى الأفق. ومع ذلك ، لو تفحصنا الأمر عن قرب ، يتكون لمعان الشمس من العديد من الانعكاسات الصغيرة للشمس. أو بريق الشمس.

ويحبذ المسطخون “محاكاة” لإظهار أن السطح المنحني لا يؤدي إلى شكل انعكاس مشابه للواقع ، وبالتالي ، استنتجوا أن “الأرض ليست كرة”. كان خطأهم هو وضع المراقب بعيدا عن سطح الأرض ، وكذا جعل الانحناء كبير لتمثيل الأرض الكروية. كانت محاكاتهم أكثر ملاءمة لوصف كيفية ظهور sunglint – انعكاس الشمس على سطح المحيط الأملس – من الفضاء.
فعلى سبيل المثال ، تبدو صور الأرض المأخوذة من ساتل هيماواري -8 مشابهة لخاصية الإنعكاس في محاكاتهم.

المحاكاة الأكثر ملاءمة لتمثيل لمعان الشمس هي الانعكاس على الطريق الرطب. الطريق ليس سلسًا تمامًا ، ولكن هناك طبقة مبللة تغطيها مياه تعكس الضوء في العديد من الاتجاهات. سيكون المراقب أيضًا قريبًا من السطح ، وبالتالي أكثر تشابهًا مع ما نحاول محاكاته. حقيقة أن الطريق مسطح ، محدب أو مقعر لا يغير خصائص الانعكاس بالكثير. ليس بقدر ما يظهر لنا هؤلاء الأشخاص المسطحون، علاوة على ذلك ، لا يكون الطريق عادة مسطحًا تمامًا ولكنه منحني قليلاً للسماح للمياه الزائدة بالإنسياب.

#مراجع

• Sun glitter – Wikipedia
• Sun glitter – The Weather Notebook
• Glittering Light on Water – Joseph A. Shaw – NOAA

هناك فيديوهات تظهر الشمس وكأنها تغرب، ولكن بعد تكبير الكاميرا، نرى الشمس لا تزال فوق الأفق، يرجع السبب في ذلك إلى أن نظام التعريض التلقائي بالكاميرا يضبط باستمرار التعريض، وفي مثل هذه المشاهد ، يوجد فرق في السطوع العام قبل التكبير وبعده.

يتخذ أصحاب الأرض المسطحة مقاطع الفيديو هذه كـ “دليل” على ابتعاد الشمس. هم مخطئون.
الأمر متعلق فقط بمسألة التصوير. في الواقع ، لا تتراجع الشمس، ولها نفس الحجم الزاوي على مدار اليوم.

أي كاميرا لديها قيود في المدى الدينامي، لا يمكن للكاميرات التقاط أجزاء مضاءة ومظلمة من المشهد إذا كان الفرق في السطوع مرتفعًا بما يكفي.، إذا كان في المشهد جسم مظلم وجسم مضاء في نفس الوقت ، فستضطر الكاميرا إلى تحديد أولويات التقاط جسم واحد وتضحي بالآخر، يمكن أن تختار التقاط الجزء المظلم ، ولكن يصبح الجسم المضاء شديد السطوع أو ذا تعريض زائد overexposed، أو يمكنه التقاط المنطقة المضيئة ، ولكن الجزء المظلم سيصبح قاتماً أو أقل سطوعاً underexposed.

في حالة غروب الشمس ، هناك منطقتان مختلفتان في شدة التباين : الشمس الساطعة جدا ، والأرض الأكثر قتامة، ستضطر الكاميرا لإعطاء الأولوية لأحدهم والتضحية بالأخر. إذا كان ضبط التعريض التلقائي في وضع التشغيل ، فستقوم معظم الكاميرات بتقييم المشهد بأكمله ، ومحاولة تحديد التعريض الأمثل لجعل معظم المشهد مرئيًا.

في وضع الزاوية العريضة (يسار) ، تكون الشمس أصغر ، وسطح البحر المظلم يسيطر على المشهد. حاولت الكاميرا تحقيق التوازن في المشهد لجعل كل المناطق في الإطار واضحة قدر المستطاع ورفعت التعريض. ونتيجة لذلك ، أصبحت الشمس والوهج المحيط بها أكثر سطوعًا أو تعريضًا للضوء.

عند هذه النقطة ، لا يمكن تمييز الشمس عن معظم الوهج المحيط بها ، مما يعطي الانطباع بأنها أكبر بكثير مما هي عليه.

عند التكبير ، تحتل الشمس جزءًا أكثر أهمية من الإطار ، وتهيمن الأجسام الأكثر سطوعًا على المشهد. حاولت الكاميرا تحقيق التوازن في المشهد من خلال تقليل التعربض. ونتيجة لذلك ، لم يعد توهج الشمس أكثر تعريضًا ، وأصبح الفرق بين الشمس و وهج الشمس أكثر وضوحًا.

لا يمكن للكاميرا سوى تخمين ما يفكر فيه المصور، في معظم الحالات ، يمكن للكاميرا القيام بعملها بشكل مناسب. ولكن عندما لا يكون ذلك ممكنا ، فإن المصور لديه خيار لتجاوزه واستخدام التعريض اليدوي. للحصول على صورة محددة بوضوح لقرص الشمس ، يمكن للمصور استخدام التعريض اليدوي، ويكون التعريض الناتج نفسه سواء بالتكبير أو بدون.

وأخيرًا وليس آخرًا ، إذا كان المصور الذي إلتقط الفيديو على إستعداد للانتظار لمدة 10 دقائق أخرى ، لنزلت الشمس تحت الأفق ، ولا يمكن لأي قدر من التكبير أن يعيد الشمس إلى المشهد.

تجربة:

يمكن إظهار تأثير ضبط التعريض التلقائي في مثل هذا المشهد بسهولة باستخدام آلة تصوير / كاميرا فيديو مع خاصية التعريض التلقائي (يجب تشغيلها بشكل افتراضي). في غرفة مظلمة ، التقط مقطع فيديو لمصدر ضوء ، مثل مصباح ، وقم بتغيير التكبير / التصغير. ﺳﺗﻘوم اﻟﮐﺎﻣﯾرا ﺑﺿﺑط اﻟﺗﻌرﯾض ﺑﺣﺳب ﻧﺳﺑﺔ الضوء اﻟذي ﯾﺷﻐﻟه في المشهد. إذا كان مصدر الضوء ساطعًا بما فيه الكفاية ، فقد يعطي هذا وهجاً وقد يعطي الانطباع أن مصدر الضوء أكبر من حجمه.

#مراجع

• Exposure (photography) – Wikipedia
• Sun Glare Makes the Sun Appear Larger

غالبًا ما نشاهد المسطحين يختلقون “نموذجًا مصغَّرًا” لتفسير ظاهرة حقيقية ويعرضونه كـ “دليل” لدعم الأرض المسطحة ويستعملونه كدليل ضد الأرض الكروية. يجب عليهم مراعاة إذا كان النموذج المصغر يشبه النموذج الحقيقي نوعا ما بطريقة معينة. إذا تأكد من ذلك ، يكفي أن يستنتج أن النموذج يفسر كيف تعمل الظاهرة في النموذج الحقيقي.

وبالعكس ، إذا كان لا يمكن تصغير النموذج الحقيقي لتفسير ظاهرة ما، فإنه يستنتج أن الظاهرة في النموذج الأصلي غير موجودة.

كانوا يسمون بالخطأ إختلاق مثل هذه النماذج “بعمل تجربة”.

بعض الأمثلة على مثل هذه “التجارب”:

*صب الماء على كرة. إذا لم لا يلتصق الماء بالكرة. يستنتجون أن مياه البحر لا ينبغي أن تلتزم بالأرض إذا كانت كروية.

*وضع ميزان إستواء مائي على سطح كرة. إذا لم يظهر الميزان إستواء، يستنتجون أن الأرض ليست كروية.

*استخدام أشكال مختلفة من معدِّل الضوء ، مثل العدسات والمرايا ، لإظهار أن الشمس يمكن لها أن تغرب على الأرض المسطحة.

من الواضح أن استنتاجاتهم خاطئة:

لا يمكن اعتبار النموذج بمثابة “دليل”.
بنفس الطريقة التي لا يمكن إستعمال نموذج الكسوف كإثبات للكسوف.

حتى إذا كان نموذج ما يعرض نفس سلوك الظاهرة، فهذا لا يعني أن الظاهرة في الواقع تعمل بنفس الطريقة في جميع الحالات.

لم يكلفوا أنفسهم أبدا عناء إثبات أن النموذج يمثل حقا الظاهرة الحقيقية. لكنهم قفزوا مباشرة إلى الاستنتاجات وأخذوا النموذج كدليل صالح.

وجود نموذج مادي مصغر ليس شرطا مسبقا. إن ملاحظة الظواهر ورصدها في الواقع هي دائمًا الدليل الأقوى.

تم تصميم أحد نماذجهم ل “شرح” ظاهرة محددة. ولكنه يتعارض مع تفسير أخر ظاهرة أخرى.

هذه الأعمال التي يسمونها “تجربة” لا تؤدي إلا إلى إظهار أنهم لا يعرفون ماذا يفعلون.

على سبيل المثال ، لدحض الجاذبية ، عليك أن تعرف كل شيء عن الجاذبية. ليس لأنهم لا يفهمون ماهية الجاذبية فإنها غير موجودة. وإذا فهموا الجاذبية حقًا ، فإنهم لن يقوموا بتجربة شبيهة بالماء على كرة ، وسوف يعتبرونها “دليلاً” على عدم وجود الجاذبية.

منطق “كيتل” أو الغلاية، هو إستعمال عدة حجج متناقضة فيما بينها لمحاولة دعم نقطة أو فكرة واحدة.

منطق “الغلاية” شائع جدا في مجتمع الأرض المسطحة. إذا واجهوا ظاهرة طبيعية يصعب تفسيرها باستخدام نموذج الأرض المسطحة ، فإنهم في الغالب يصممون “نماذج تجريبية” ل “شرح” كيف يمكن أن تحدث هذه الظاهرة على أرض مستوية.

المشكلة؟ هذه النماذج تتعارض مع بعضها البعض.

المثال 1: في الأرض المسطحة ، لا يتم تقسيم مساحة الأرض التي تكون في وضح النهار وضوء الليل بالتساوي. الحل: أنشأوا نموذجًا أرضيًا مسطحًا به قبة زجاجية واستخدموا مصباحًا كشاف الشمس.

مثال 2: في تجارب “عصا الظل” من عدة مواقع ، لا تتلاقى أشعة الشمس عند نقطة واحدة في الشمس. الحل: أنشأوا نموذجًا باستخدام عدسة مقعرة بين الشمس والسطح.

مثال 3: لا يمكن أبداً أن يحدث غروب الشمس على الأرض المسطحة. الحل: قاموا بإنشاء نموذج باستخدام عدسة فريسنل Fresnel بين الشمس والمراقب.

كل هذه “الحلول” يمكن أن “تفسر” ظاهرة واحدة فقط ولكنها تتعارض مع بعضها البعض. هذه “الحلول” لا يمكن أن تتعايش على الأرجح.

لا يمكن اعتبار هذه “النماذج التجريبية” إلا فرضيات. لم يثبتوا بعد ما إذا كانت النماذج تمثل الواقع. لكنهم قفزوا إلى الاستنتاجات واتخذوا النماذج “دليلا” على الأرض المسطحة. حتى مع أخذ هذه كافتراضات فهي بعيدة جدا. يجب أن تكون أي فرضية متوافقة مع جميع الملاحظات المرتبطة بها ، أو على الأقل لا تكون متعارضة.

يسعد المسطحين بإختراع “شرحًا” محددًا لكل ظاهرة محددة ، وإذا نشأت مشكلة أخرى ، فإنهم سيضيفون “تفسيرًا” آخر، إلخ. وفي نفس الوقت ، فإن معظم هذه “التفسيرات” في صراع ولا يمكن أن تتعايش.

وبعبارة أخرى ، يستخدمون منطق “الغلاية” kettle لتقديم حججهم ، بحيث تكون التفسيرات غير صالحة.

#مراجع
Kettle logic – Wikipedia
Kettle logic – Logically Fallacious

في القرن الحادي عشر ، نجح البيروني في تحديد نصف قطر الأرض بقياس إنخفاض الأفق من أعلى التل.

في القرن الواحد والعشرين ، يمكننا بسهولة تكرار نفس التجربة بدون أي جهد. كل ما نحتاج إليه هو هاتف ذكي وفرصة مراقبة الأفق على علو شاهق ، مثل أثناء الطيران.

نفذ البيروني قياسه على مرحلتين.

أولاً : قاس أولا ارتفاع الجبل. أخذ قياسين للزاوية في قمة الجبل في مكانين مختلفين. من النتائج ، كان قادرا على تحديد ارتفاع الجبل.

ثانياً : صعد إلى قمة الجبل وقاس إنخفاض الأفق. من زاوية الانخفاض وارتفاع الجبل ، كان قادرا على حساب نصف قطر الأرض.

باستخدام التكنولوجيا الحديثة ، يمكننا القيام بنفس القياسات وتحديد بأنفسنا نصف قطر الأرض. في الوقت الحاضر ، تم تجهيز جميع الهواتف الذكية تقريبًا بجهاز GPS وهو قادر على قياس الارتفاع ويمكننا تخطي الخطوة الأولى التي قام بها البيروني. وبإستعمال مستشعرات التسارع accéléromètre المركبة داخل هواتفنا ، يمكننا قياس إنخفاض الأفق. باستخدام الهاتف الذكي الذي نحمله يوميا في كل مكان ، يمكننا إجراء قياسات البيروني. نحتاج فقط إلى أن نكون في مكان عالٍ بما يكفي وأن يكون لدينا رؤية واضحة للأفق ، كما هو الحال أثناء الطيران.

تأكد من تثبيت التطبيق بالفعل قبل الصعود ، وبطبيعة الحال ، لا تنسى أن تحجز مقعد النافذة! القياس من خلال المحيط يكون أكثر دقة. وإذا كنا لا نثق بمعلومات الإرتفاع للهواتف الذكية لدينا، يمكننا أن نسأل دائما المضيفات أو استخدام نظام الترفيه على متن الطائرة IFE.

تطبيقات

فيما يلي بعض التطبيقات التي يمكننا استخدامها لإجراء القياس.

Theodolite (iOS)
Dioptra (Android)
Geocam (Android)
Surveyor Tools (Android)

حساب

الحساب باستخدام الأرقام الواردة في الرسم التوضيحي:

38805 قدم * cos (3.4 درجة) / (1 – cos (3.4 درجة)) بالكيلومتر = 6707.8 كم
38805 ft * cos (3,4 degrés) / (1- cos (3,4 degrés)) en km = 6707,8 km

لا تختلف النتيجة إلا عن 5٪ من القيمة الفعلية.

اشتقاق المعادلة

#مراجع
Al-Biruni’s Classic Experiment: How to Calculate the Radius of the Earth – Owlcation
The Empire of Reason 3/6 (Science and Islam – Episode 2 of 3) – Jim Al-Khalili – BBC
How Al-Biruni Calculated the Circumference of the Earth Using a Mountain in the 11th Century – Flat Earth Busted

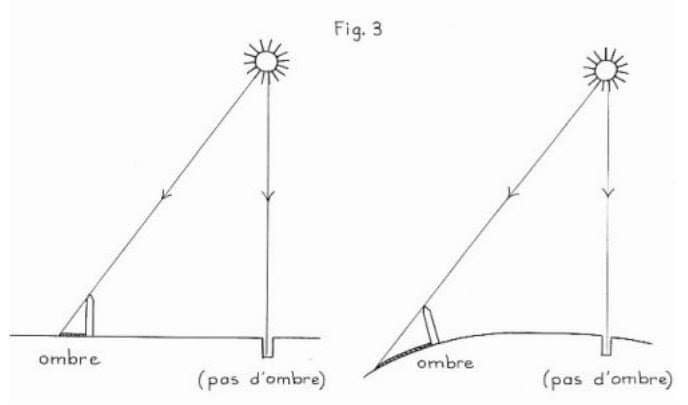
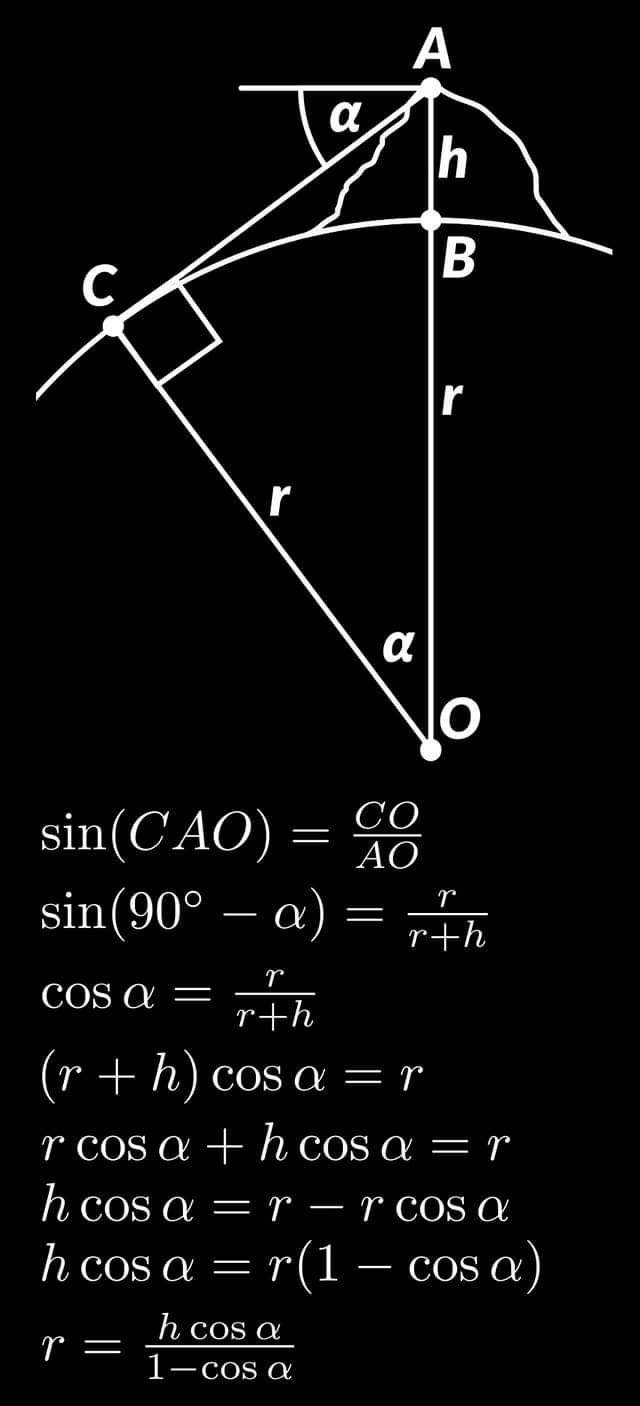
في عام 205 قبل الميلاد ، نجح إراتوستينس في تحديد محيط الأرض عن طريق قياس طول الظل الناتج قضيب. قام بإجراء القياس في الإسكندرية وتزامن ذلك مع اللحظة التي تكون فيها الشمس متعامدة على أصوان.

بعد 2222 سنة ، حاول المسطحين تفنيد تجربة إراتوستينس. يقولون أن التجربة يمكن تطبيقها على نموذج الأرض المسطحة.

استنسخت الصورة بطلب من نوقع Eratosthenes.eu

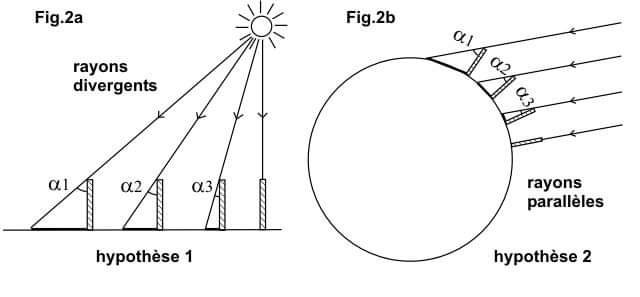
في الرسم البياني أعلاه صورة رقم 2، هذين الرسمان صحيحان:

إذا افترضنا أن الأرض كروية وأن الشمس بعيدة ، يمكننا تحديد محيط الأرض (الصورة اليمنى).

إذا افترضنا أن الأرض مسطحة وأن أشعة الشمس ليست متوازية ، يمكننا تحديد المسافة إلى الشمس (الصورة اليسرى).

باستخدام نموذج الأرض المسطحة ، خلصوا إلى أن المسافة إلى الشمس ليست سوى على إرتفاع 3000 إلى 5000 كيلومتر (1850 إلى 3100 ميل).

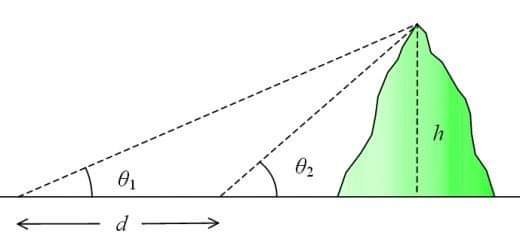
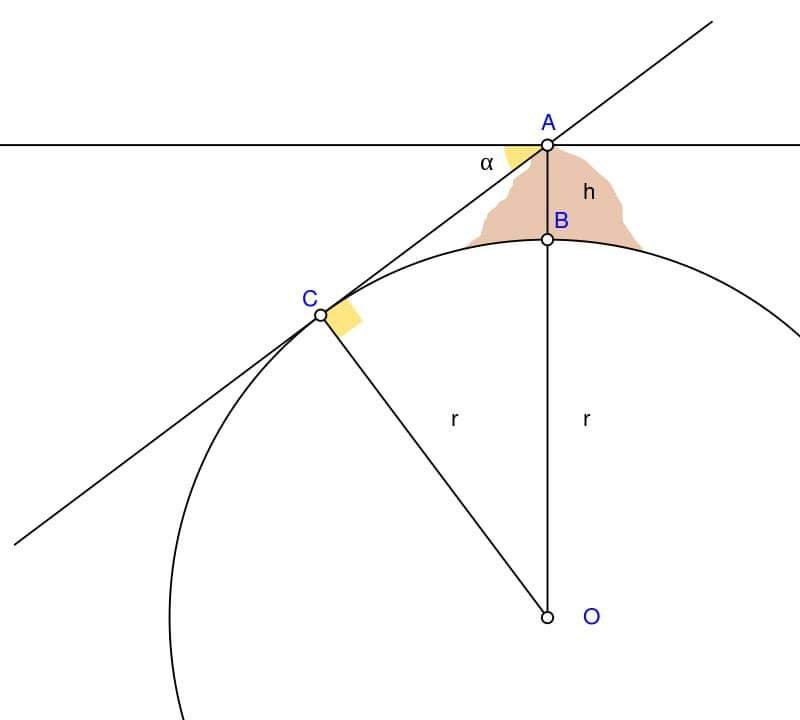
قام إيراتوستينس بتجربته بأخذ القياسات من مكانين فقط: الإسكندرية وأصوان. ولكن يمكننا بسهولة تعديل تجربته عن طريق أخذ القياسات في ثلاثة أماكن أو أكثر ، وإثبات نموذج الأرض المسطحة على الفور أنه خطأ.

استنسخت الصورة بطلب من موقع Eratosthenes.eu

باستخدام نموذج الأرض المسطحة ، سيكون لطول الظل استجابة خطية linear response . من ناحية أخرى ، باستخدام نموذج الأرض الكروية ، فإن طول الظل له استجابة غير خطية non-linear response.

يمكننا أيضًا ملاحظة أنه في المناطق القريبة من الدائرة القطبية ، تعطي التجربة ظلًا طويلاً جدًا. لا يمكن لنموذج الأرض المسطحة تفسير هذه الظاهرة.

بالإضافة إلى ذلك ، لن يعطي نموذج الأرض المسطحة نتائج متوافقة، ليس من الصدفة أن المسطحين لا يمكنهم الحصول على المسافة الدقيقة للشمس. سوف تختلف نتائجهم كثيرًا حتى إذا لم تتطلب هذه التجربة دقة كبيرة.

وبسبب هذا ، يمكننا أن نستنتج بسهولة أن الأرض كروية وليست مسطحة.

يمكنك إجراء الحساب بنفسك دون السفر باستخدام البيانات المقدمة من Eratosthenes.eu. يحاول هذا الموقع الإلكتروني التنسيق مع مدرستين حول العالم ومساعدتهما على إعادة تجربة إراتوستينس كمنهج تعليمي. بياناتهم متاحة للجمهور ويمكن استخدامها لأغراضنا.

#مراجع
Flat Earth Insanity: Simple Proof for Convexity of Earth – Flat Earth Disproved
Eratosthenes.eu